機械学習の基礎を学ぶための「機械学習入門」。以下のページを参考にして、日本語解説を加えました。ソースコードは以下にあります。
前回までで、モデルの精度を評価する方法を学びました。今回は、学習不足(アンダーフィッティング)と過学習(オーバーフィッティング)の概念を理解します。
決定木モデルの自由度
scikit-learnのドキュメントを見ると、決定木モデルには多くのオプションがあることがわかります。決定木の深さなど、決定木に関するいくつものオプションがあることがわかります。つまり、モデルを好きな形に変形できる自由度があるということです。
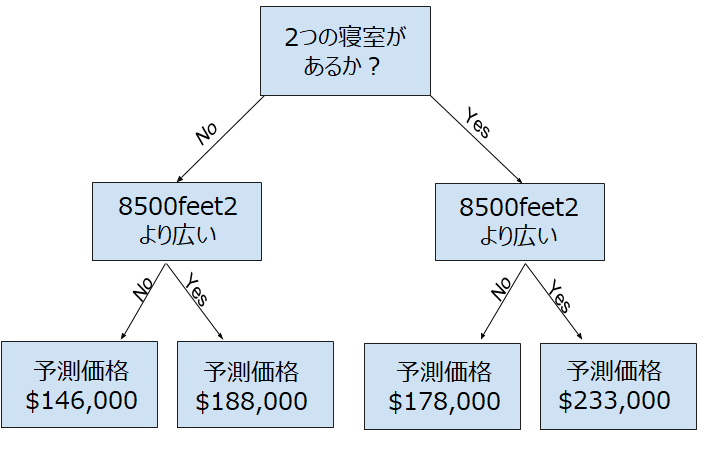
上の決定木は前回までに示した住宅価格に関する決定木です。実際には、決定木が10個の分割があることもよくあります。木が深くなるにつれて、データセットに含まれる家は、それぞれの枝分かれした先に分割されます。機械学習モデルの決定木では、この枝分かれの数をオプションで指定することもできます。
過学習と学習不足
各レベルで分割を追加してグループの数を2倍にし続けると、10レベルに到達するまでに210のグループができます。データを多くの葉(leaf)に分けると、各葉のデータも少なくなります。データ数が非常に少ないグループは、グループ内の家の価格を高い精度で予測できますが、新しいデータについては信頼性の低い予測を行う可能性があります(各予測は少数のデータにのみ基づいているため)。これは過学習・過剰適合(オーバーフィッティング)と呼ばれる現象です。
逆に、グループを2つまたは4つに分割する場合、各グループのデータは完全に分割されておらず、結果として得られる予測は、トレーニングデータであっても精度が不十分であることがあります。モデルがデータ内の重要な区別やパターンを認識できていないためであり、これはアンダーフィッティングと呼ばれます。
ちょうどよい学習状態とは
オーバーフィッティングとアンダーフィッティングの中間にある、ちょうどよい学習状態とはどこでしょうか。
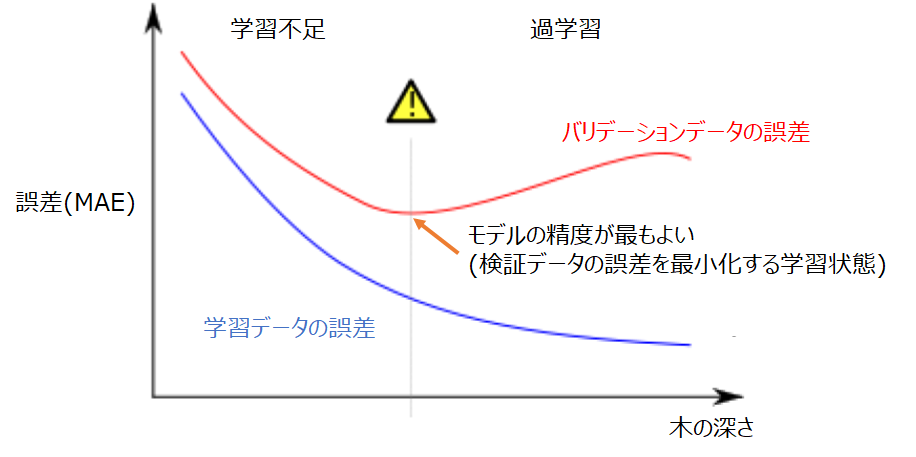
グラフにすると、赤色のバリデーション曲線の、誤差が最小となる点が重要になります。モデルが未知のデータ(バリデーションデータ)を高い精度で予測できることに価値があります。つまり、バリデーションデータにおいて誤差を最小化する学習状態を目指す必要があります。
決定木モデルでの実践
ツリーの深さを制御する方法はいくつかあります。1つの方法として、ツリーを通る一部のルートの深さを他のルートよりも大きくする方法があり、max_leaf_nodes引数で制御します。モデルに作成できる決定木の葉が多い(max_leaf_nodes)ほど、上のグラフの右側(過剰適合領域)に移動しますので、適切なmax_leaf_nodesの値が存在するはずです。
ユーティリティ関数を使用して、max_leaf_nodesのさまざまな値からのMAEスコアを比較できます。
from sklearn.metrics import mean_absolute_error
from sklearn.tree import DecisionTreeRegressor
def get_mae(max_leaf_nodes, train_X, val_X, train_y, val_y):
model = DecisionTreeRegressor(max_leaf_nodes=max_leaf_nodes, random_state=0)
model.fit(train_X, train_y)
preds_val = model.predict(val_X)
mae = mean_absolute_error(val_y, preds_val)
return(mae)前回までにすでに書いた以下のコードを使用して、train_X、val_X、train_y、val_yを定義します。データは下記の場所からダウンロードできます。

import pandas as pd
melbourne_file_path = '../input/melbourne-housing-snapshot/melb_data.csv'
melbourne_data = pd.read_csv(melbourne_file_path)
filtered_melbourne_data = melbourne_data.dropna(axis=0)
y = filtered_melbourne_data.Price
melbourne_features = ['Rooms', 'Bathroom', 'Landsize', 'BuildingArea',
'YearBuilt', 'Lattitude', 'Longtitude']
X = filtered_melbourne_data[melbourne_features]
from sklearn.model_selection import train_test_split
train_X, val_X, train_y, val_y = train_test_split(X, y,random_state = 0)forループを使用して、max_leaf_nodesのさまざまな値で構築されたモデルの精度を比較します。
for max_leaf_nodes in [5, 50, 500, 5000]:
my_mae = get_mae(max_leaf_nodes, train_X, val_X, train_y, val_y)
print("Max leaf nodes: %d \t\t Mean Absolute Error: %d" %(max_leaf_nodes, my_mae))Max leaf nodes: 5 Mean Absolute Error: 347380
Max leaf nodes: 50 Mean Absolute Error: 258171
Max leaf nodes: 500 Mean Absolute Error: 243495
Max leaf nodes: 5000 Mean Absolute Error: 254983
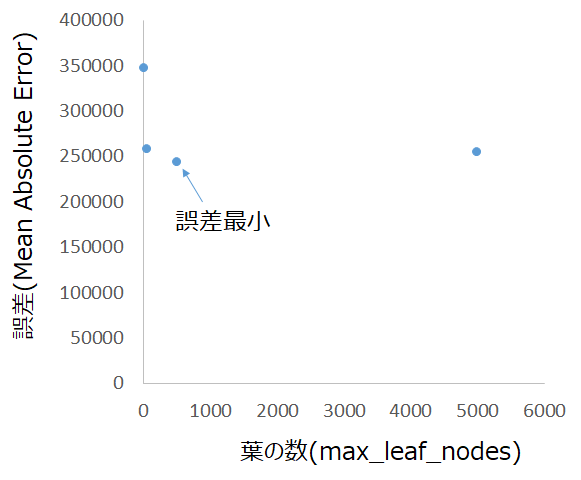
結果として、max_leaf_nodesを500とすると最も誤差が小さくなりますが、葉の数が増えすぎると
まとめ
過学習と学習不足は、
過学習:偽のパターンを学習し、予測の精度を低下
学習不足:そもそもパターンの学習に失敗し、予測の精度が低下
であり、モデルの工夫(今回は決定木のオプション)でこれらを回避できます。
次回は、決定木を拡張したランダムフォレストについて学びます。
コメント