ChatGPTがプログラミングが可能です。私も、batファイルやpythonプログラムを作る手間が省け、業務効率が改善しています。
もっと「ガチ」な用途にも使えるのだろうかと考え、燃料電池の発電性能を予測するためのプログラムを書いてもらいました。
燃料電池とは

燃料電池は、水素と酸素を結合させて電気を作る発電機のようなものです。
燃料電池スタックの中には、アノードとカソードと呼ばれる2つの電極と、電解液と呼ばれる特殊な物質があります。アノードに水素ガスを、カソードに空気中の酸素を供給すると、化学反応が起こり、電気と水が作られます。
燃料電池スタックで作られた電気は、車の電気モーターの動力となり、車輪を回して車を走らせます。そして、車の排気ガスから出るのは水蒸気だけで、従来のガソリン車の排気ガスよりもずっと環境にやさしいと言われています。
燃料電池の発電性能は、反応効率や燃料電池スタックの設計、運転条件など、いくつかの要因で決まります。発電性能の理論式は「ネルンストの式」や「Butler-Volmerの式」で定義されます。これらヒントを与えて、ChatGPTがどんなプログラムを出してくるか見てみましょう。
ChatGPTにお願いしてみる
投入したクエリは以下の通りです。
燃料電池の発電性能を予測するプログラムを書いてください。バトラー・ヴォルマー方程式を使って電圧損失を解く、pythonでお願いします。ガス濃度、流量、その他必要な情報をお願いします。
プログラムによる数値の定義に変更する必要があります。
電流密度の単位を A/cm^2 で定義できるように変更する。
gas_concentrationの値を、酸素濃度、水素濃度の体積分率でそれぞれ定義できるようにする。
空気利用率、燃料利用率を入力することで流量が算出できるようにする。
出てきたプログラムは以下の通りです。
pythonプログラム
import numpy as np
# Function to calculate the voltage loss using the Butler-Volmer equation
def calc_voltage_loss(i, k, t, a, b, c):
"""
i: current density (A/cm^2)
k: exchange current density (A/m^2)
t: temperature (K)
a: transfer coefficient (dimensionless)
b: reactant concentration at electrode surface (mol/cm^3)
c: reactant concentration in bulk solution (mol/cm^3)
"""
r = 8.314 # gas constant (J/mol*K)
f = 96485 # Faraday's constant (C/mol)
term1 = (a*f*i)/(2*r*t)
term2 = np.log((k*b)/(k*c))
return term1*term2
# Define input values
gas_concentration_oxygen = 0.21 # volume fraction of oxygen
gas_concentration_hydrogen = 0.79 # volume fraction of hydrogen
flow_rate_air_utilization = 1.5 # air utilization rate
flow_rate_fuel_utilization = 1.2 # fuel utilization rate
current_density = 500 # A/cm^2
temperature = 373 # K
transfer_coefficient = 0.5 # dimensionless
electrode_surface_concentration = 0.05 # mol/cm^3
bulk_solution_concentration = 0.1 # mol/cm^3
# Calculate gas concentration in mol/cm^3
gas_concentration = (gas_concentration_oxygen + gas_concentration_hydrogen) * 1000/22.4 # assuming ideal gas behavior
# Calculate flow rate in mol/s
flow_rate = (flow_rate_air_utilization * 0.21 + flow_rate_fuel_utilization * 2) * gas_concentration
# Convert current density to A/cm^2
current_density /= 10000
# Calculate exchange current density
exchange_current_density = gas_concentration * flow_rate
# Calculate voltage loss using the Butler-Volmer equation
voltage_loss = calc_voltage_loss(current_density, exchange_current_density, temperature, transfer_coefficient, electrode_surface_concentration, bulk_solution_concentration)
print("The voltage loss is: ", voltage_loss, "V")このプログラムを実行すると、以下のような値が出力されます。
The voltage loss is: -0.26957301952457174 V
電圧ロスの値としては、まあ悪くない結果を返してきたのではないでしょうか。素晴らしいです。
calc_voltage_lossでButler-Volmer式を解いて、電圧ロス(損失)を予測しています。
物性値の中で、transfer_coefficientやelectrode_surface _concentrationなどのよくわからないパラメータを定義しているので、聞いてみました。
What do the following properties mean?
transfer_coefficient = 0.5 # dimensionless
electrode_surface_concentration = 0.05 # mol/cm^3
bulk_solution_concentration = 0.1 # mol/cm^3
回答: transfer_coefficientは、電極表面での電子移動過程を記述するButler-Volmer方程式における無次元パラメータである。全オーバポテンシャルのうち、活性化損失によるものの割合を示す。一般的には0.1~0.7程度で、0.5程度がよく使われる値である。 electrode_surface_concentration は、電極表面の反応物濃度で、通常mol/cm^3 で測定されます。このパラメータは、反応のキネティクスと交換電流密度に影響します。表面濃度が高いほど、反応速度と交換電流密度が高くなります。 bulk_solution_concentration はバルク溶液中の反応物濃度で、通常 mol/cm^3 で測定されます。このパラメータは、電極表面への反応物の輸送と濃度分極に影響します。バルク濃度が高いほど、反応物の輸送速度が高くなり、濃度分極が低くなります。
なんとなくそれっぽい説明をしてくれました。
transfer_coefficientが活性化損失によるものの割合、というのは、言葉と中身が一致していないように思います。
そもそも、損失の割合を入力で決めるのはナンセンスだと思ったので、各分極での損失を分けられないか検討させてみました。
損失をより細かく算出させる
以下のような回答とともに、プログラムが出力されました。
回答: 各分極での損失を分離するために、Butler-Volmer方程式を修正し、活性化損失、濃度損失、オーミック損失の別々の項を含めることができます。活性化損失は移動係数と活性化エネルギーに、濃度損失は電極表面とバルク溶液中の反応物濃度に、オーミック損失は電解液と電極の抵抗に関連する。そして、総電圧損失に対する各損失の寄与度を計算することができます。 ここでは、活性化損失、濃度損失、オーミック損失について別々の用語を含むプログラムの更新版を紹介します。
import numpy as np
import matplotlib.pyplot as plt
# Constants
R = 8.3145 # J/(mol*K)
F = 96485 # C/mol
T = 298 # K
# Parameters
A = 1 # cm^2
transfer_coefficient = 0.5 # dimensionless
electrode_surface_concentration = 0.05 # mol/cm^3
bulk_solution_concentration = 0.1 # mol/cm^3
electrolyte_resistance = 0.1 # Ohm*cm^2
gas_diffusion_coefficient = 1e-5 # cm^2/s
cathode_flow_rate = 2 # cm^3/min
anode_flow_rate = 2 # cm^3/min
fuel_utilization_rate = 0.5 # dimensionless
air_utilization_rate = 1 # dimensionless
# Calculate gas concentrations
oxygen_concentration = bulk_solution_concentration * air_utilization_rate
hydrogen_concentration = bulk_solution_concentration * fuel_utilization_rate
# Calculate flow rate
flow_rate = (cathode_flow_rate + anode_flow_rate) / 60 # cm^3/s
# Calculate exchange current density
exchange_current_density = (gas_diffusion_coefficient * F * (oxygen_concentration - hydrogen_concentration) / (R * T)) ** 0.5
# Initialize arrays
current_density_array = np.linspace(0.1, 5, 50) # A/cm^2
voltage_array = np.zeros_like(current_density_array)
ohmic_loss_array = np.zeros_like(current_density_array)
activation_loss_array = np.zeros_like(current_density_array)
concentration_loss_array = np.zeros_like(current_density_array)
ocv_array = np.zeros_like(current_density_array)
# Loop over current densities
for i in range(len(current_density_array)):
# Calculate the anode and cathode overpotentials
eta_anode = current_density_array[i] * electrolyte_resistance / (2 * F)
eta_cathode = current_density_array[i] * electrolyte_resistance / (2 * F)
# Calculate the activation loss
activation_loss = transfer_coefficient * R * T / F * np.log(current_density_array[i] / exchange_current_density)
activation_loss_array[i] = activation_loss
# Calculate the concentration loss
concentration_loss = R * T / (transfer_coefficient * F) * np.log((oxygen_concentration * hydrogen_concentration) / (electrode_surface_concentration ** 2))
concentration_loss_array[i] = concentration_loss
# Calculate the ohmic loss
ohmic_loss = current_density_array[i] * electrolyte_resistance
ohmic_loss_array[i] = ohmic_loss
# Calculate the total voltage loss and OCV
voltage_loss = activation_loss + concentration_loss + ohmic_loss
voltage_array[i] = voltage_loss
ocv_array[i] = voltage_loss + eta_anode + eta_cathode
# Plot results
fig, ax1 = plt.subplots()
color = 'tab:red'
ax1.set_xlabel('Current Density (A/cm$^2$)')
ax1.set_ylabel('Total Voltage Loss (V)', color=color)
#ax1.plot(current_density_array, voltage_array, color=color)
#ax1.plot(current_density_array, ocv_array,
#color='tab:blue', linestyle='--')
ax1.plot(current_density_array, ohmic_loss_array, label='Ohmic Loss', color='tab:red')
ax1.plot(current_density_array, concentration_loss_array, label='Concentration Loss', color='magenta')
ax1.plot(current_density_array, activation_loss_array, label='Activation Loss', color='green')
ax1.tick_params(axis='y', labelcolor=color)
ax1.legend(loc='upper left')
plt.title('Fuel Cell Polarization Curve')
plt.show()
# Plot results
fig, ax1 = plt.subplots()
color = 'tab:red'
ax1.set_xlabel('Current Density (A/cm$^2$)')
ax1.set_ylabel('Voltage (V)', color=color)
ax1.plot(current_density_array, voltage_array, color=color, label='voltage')
ax1.plot(current_density_array, ocv_array,
color='tab:blue', linestyle='--', label='ocv')
ax1.legend(loc='upper left')
plt.title('Fuel Cell Polarization Curve')
plt.show()このプログラムを実行すると、以下のような結果が出力されます。
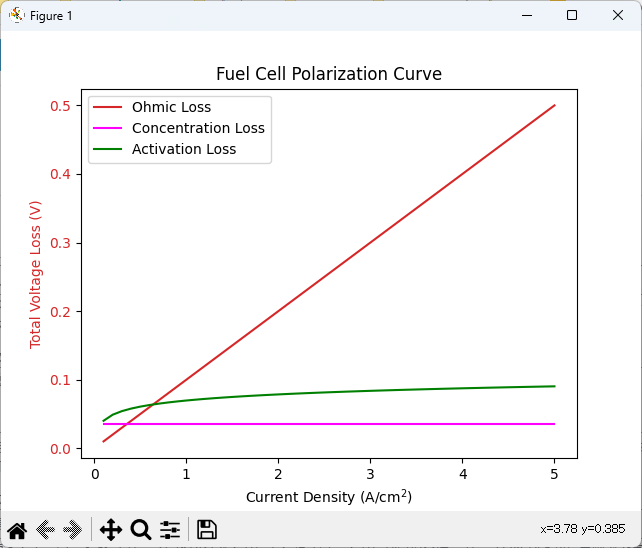
電流密度にしたがって、電圧ロスがそれぞれ増加していくことが分かります。
絶対値の正確さはおいておいて、それっぽい結果が出力されました。
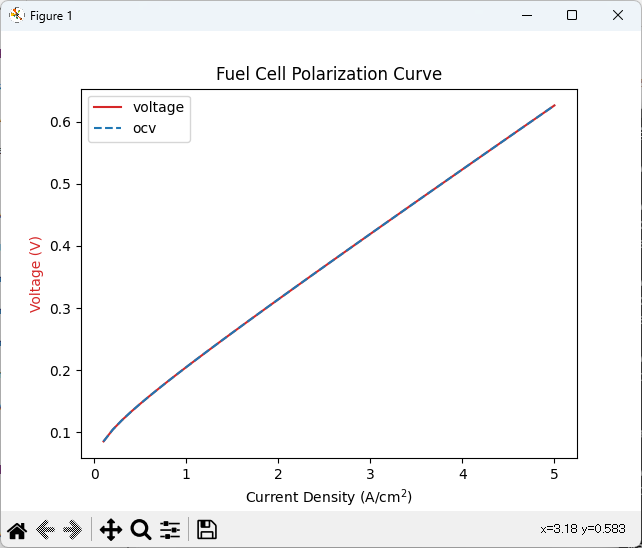
ただ、OCVと電圧が一致するという意味不明な結果になります。
コードを読んでみると、voltage_arrayは、過電圧の合計値であることがわかります。惜しいですね。
まとめ
数式を定義して計算する、といった作業は問題なく可能なようです。
一方で、その数式や式定義は不正確な部分もあります。
どのような式を解けばよいかわかっている状態で、プログラムが意図したとおりに動いていることを確認できるのであれば、シミュレーションのプログラムをChatGPTに書かせるのはアリかも。
今回の燃料電池の発電性能を予測するシミュレーションも、考慮すべき現象やパラメータなどは無限にあります。このプログラムだけで実用に耐えるわけはありませんが、この方法で少しずつ技術を積み上げていくと、もしかするとChatGPTだけでコーディングされたシミュレーションソフトウェアが完成するかもしれません。
コメント