統計解析の最も初歩的なテーマとして、重回帰が挙げられます。
複数の説明変数から、目的変数を線形回帰で説明する重回帰は、統計的な概念や技術を含んでいるため、人によっては難しいと感じる人もいます。
一方で、しっかり学んで活用すれば、重回帰は理解しやすいモデルになりえます。本稿では、重回帰の理解と、pythonでの実装を目的とします。
重回帰分析とは
ある日上司から「とりあえず重回帰でデータ分析してみて」と言われました。重回帰って何だっけ…どうやるんだっけ…と、統計の教科書を引っ張り出して調べました。
重回帰分析(multiple regression)とは、説明変数と二つ以上の目的変数との関係を探る統計的手法です。目的変数と説明変数の間の線形関係を特定し、他の説明変数を制御しながら、目的変数に対する各目的変数の効果を推定します。
重回帰分析では、目的変数をY、説明変数をX1、X2、…、Xnと表記することが多く、重回帰の式は、次のように書くことができます。
Y = b0 + b1X1 + b2X2 + …. + bnXn + ε
ここで b0 は定数項(切片とも)、b1 から bn は回帰係数(スロープ係数とも)、ε は誤差項です。
誤差項は,説明変数によって説明されない目的変数の変化ぶんを表現しますが、今回は議論しません。
memo 例えば、自動車のエンジンを設計する場合、エンジンの性能を最適化するために、シリンダーの大きさ、燃料噴射装置、吸気装置など、さまざまな要素を考慮する必要があります。重回帰分析では、さまざまな説明変数(シリンダーの大きさ、燃料噴射装置、吸気装置など)を考慮し、それらが目的変数(エンジンの性能)に与える影響を調査します。重回帰分析によって、どの説明変数が目的変数に最も大きな影響を与えるかを特定し、他の説明変数を最適化して目的の結果を得ることができます。
pythonによる重回帰分析
pythonで重回帰を記述すると、このようなコードで書けます。
import numpy as np
import statsmodels.api as sm
# create data--------------------------------------------------------------------
# x:説明変数6x3のnumpy配列として定義する
X = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[10, 11, 12],
[13, 14, 15],
[16, 17, 18]])
# y:目的変数6x1のnumpy配列として定義
y = np.array([[10],
[20],
[30],
[40],
[50],
[60]])
# end of create data---------------------------------------------------------------
# 定数を説明変数に加える
# 切片項の説明変数に 1 の列を追加する(※)
X = sm.add_constant(X)
#データを表示
print("Independent Variables (X):\n", X) # print independent variables
print("\nDependent Variable (y):\n", y) # print dependent variable
# 線形回帰でモデルをフィッティングする
# 目的変数 y と説明変数 X で OLS 回帰モデルを適合させる。
model = sm.OLS(y, X).fit()
# print model summary
print("\nModel Summary:\n", model.summary()) # print summary of the regression model説明変数3つと、目的変数1つが、それぞれ6水準存在するデータを用いて重回帰をしています。
データをランダムに作成する場合は、create data欄を以下のようなコードに置換してください。重回帰に用いるデータは、説明変数をランダムに生成、目的変数を説明変数から作成しています。
# create data--------------------------------------------------------------------
data_num = 500
np.random.seed(123) # set seed for reproducibility
X = np.random.randn(data_num, 3) # 3つの説明変数の観測値を200個生成する
# 説明変数にノイズを加えた線形結合として目的変数を生成する
y = np.dot(X, [1.5, 2.5, 3.5]) + np.random.randn(data_num) * 0.5
# end of create data--------------------------------------------------------------------今回の重回帰では、OLSと呼ばれる回帰モデルを用いて適合させています。
OLSとは「ordinary least squares」の略で、線形回帰モデルのパラメータを推定するための手法です。OLSでは、”予測値と目的変数の二乗差の和”を最小にする係数を求めます(最小二乗法を用います)。
重回帰モデルには、他にもリッジ回帰、ラッソー回帰、エラスティックネット回帰などがあります。これらの方法は、OLSの仮定が満たされない場合や、説明変数間に多重共線性(説明変数間の相関が強い)がある場合に使用されることが多いです。
今回、OLS モデルを選択した理由は、線形回帰モデルのパラメータを推定する方法として広く使われており、線形性、独立性、均等分散性、正規性の仮定が満たされている場合に適切であるためです。さらに、OLSは実装と解釈が比較的簡単でもあります。
(※) 重回帰で説明変数に1を加えることは、「センタリング」または「平均値センタリング」と呼ばれる一般的なテクニックです。説明変数をセンタリングする目的は,切片項の解釈をより意味のあるものにすることです。 説明変数がセンタリングされていない場合、切片項は、すべての説明変数が0であるときの目的変数の予測値を表します。しかし,説明変数がセンタリングされると、切片項は、中心化された独立変数がその平均値であるときの目的変数の予測値を表わします。 説明変数がセンタリングされることで、切片項は説明変数がその平均値にあるときの目的変数の予測値を表し、これは説明変数がセンタリングされていないときよりも意味のある解釈ができます。さらに、センタリングは回帰アルゴリズムの数値的安定性を向上させ、回帰係数をより容易にする効果もあります。
モデルの適合結果
重回帰のpythonコードを実行すると、重回帰モデルのサマリーに以下のような結果が出力されます。
Model Summary:
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.993
Model: OLS Adj. R-squared: 0.992
Method: Least Squares F-statistic: 758.7
Date: Sat, 25 Feb 2023 Prob (F-statistic): 1.88e-17
Time: 06:22:38 Log-Likelihood: -13.923
No. Observations: 20 AIC: 35.85
Df Residuals: 16 BIC: 39.83
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -0.1058 0.129 -0.820 0.424 -0.379 0.168
x1 1.4938 0.112 13.302 0.000 1.256 1.732
x2 2.4910 0.098 25.474 0.000 2.284 2.698
x3 3.5003 0.115 30.312 0.000 3.256 3.745
==============================================================================
Omnibus: 1.062 Durbin-Watson: 2.236
Prob(Omnibus): 0.588 Jarque-Bera (JB): 0.786
Skew: -0.080 Prob(JB): 0.675
Kurtosis: 2.042 Cond. No. 1.70
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
以下は、結果の中で我々が着目すべき点です。
coef
回帰の要約出力では、”coef” 列は、各説明変数の推定回帰係数を表示します。X3の推定係数は3.5003で、他の説明変数(X1、X2)の係数より大きい結果が得られました。
coefの最も大きいX3は、目的変数に最も高い影響を与えるようです。これは、他のすべての変数を一定にすると、X3の1の増加は、目的変数が3.5003増加すること意味します。
重回帰による予測式は、以下のようなものになります。
y = b0 + b1*x1 + b2*x2 + b3*x3
定数項(b0)は -0.1058、説明変数1の係数(b1)は 1.4938、説明変数2の係数(b2)は 2.4910、独立変数3の係数(b3)は 3.5003 となります。
memo 統計学では、説明変数は独立変数、目的変数は従属変数とも呼ばれます。機械設計の現場では、統計学よりも工学の用語を使うことが多く、説明変数Xや目的変数Y、といった表現をすることが多いです。高額でも従属変数という用語は用いられますが、従属変数が説明変数となる場合に用いられることが多く、最終的に求めたいYの値を目的変数(or目的関数)と呼んでいます。
R2乗と調整済みR2乗
R-squared(R2乗)とAdj. R-squared(調整済みR2乗)は、説明変数が目的変数の変動をどれだけよく説明するかの尺度です。
R2乗は、説明変数によって説明される目的変数の変動の割合であり、修正済みR2乗は、モデル中の説明変数の数を考慮に入れます。この場合、R2乗は0.993、修正済みR2乗は0.992で、これはモデルがデータによく適合し、説明変数が目的変数の変動のほとんどを説明することを示しています。
F-statisticとProb(F-statistic)
F-statistic(=F統計量)は、回帰モデルの全体的な有意性を測定し、Prob (F-statistic) は、F統計量に関連するp-値である。この場合、F-statistic は 758.7 であり、Prob (F-statistic) は非常に小さい(1.88e-17) 。これはモデルが統計的に有意であることを示している。
係数の推移 係数(coef)各説明変数の推定回帰係数と切片項(const)を示している。標準誤差 (std err) は推定された係数のばらつきを示し,t 値は各係数の有意性を示す.p値(P>|t|)は各係数の統計的有意性を示し、p値が小さいほど統計的に有意な係数を示している。この場合、すべての係数は非常に小さなp値(0.001未満)で統計的に有意である。
Cond No(コンディション・ナンバー)
これは説明変数間の多重共線性の尺度である。結果のCond Noは1.7と小さく、説明変数間の多重共線性がないことを示します。コンディションナンバーが高い場合(30以上)、多重共線性が見られる(=説明変数がお互いに高い相関を持っている)ことを示します。多重共線性が影響すると、回帰係数の推定値が不安定になり、分析結果の解釈が難しくなることがあります。
要約すると、モデルの全体的な適合度と統計的有意性を決定するためのR2乗、F統計量、p値、および目的変数に対する各説明変数の寄与度を決定するための係数に注目する必要があるということです。
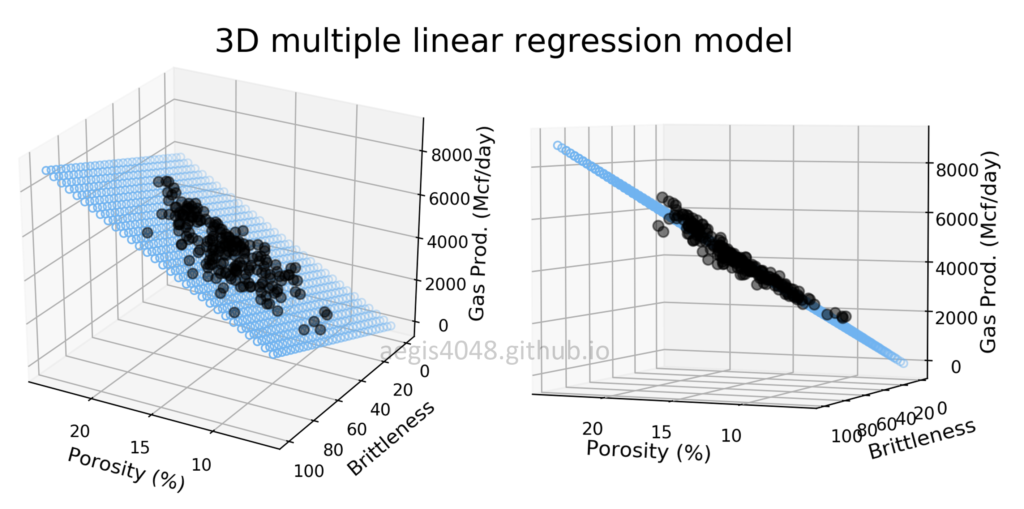
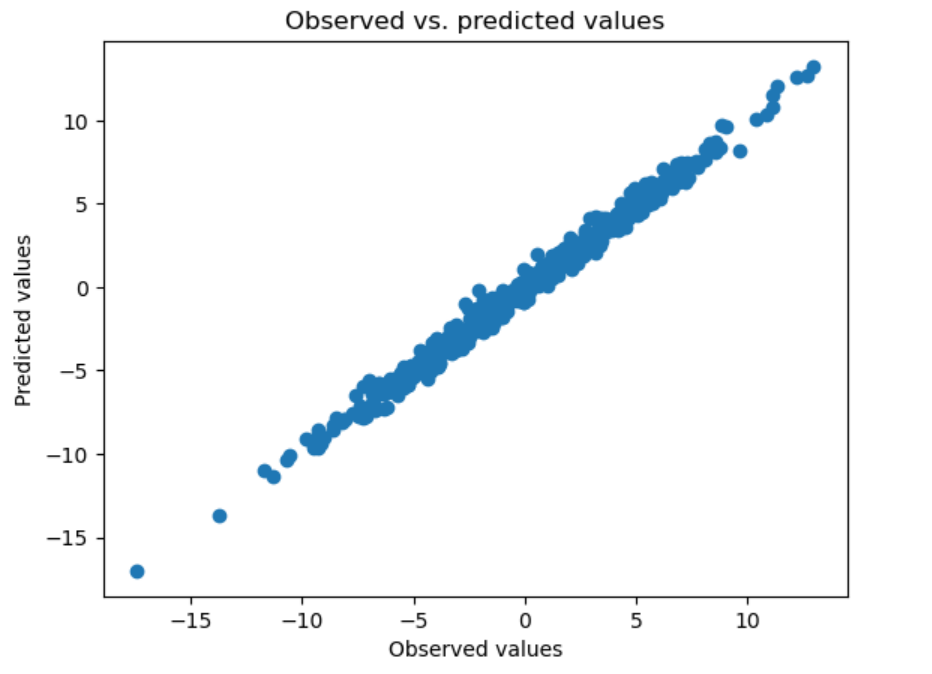
結果の可視化
import matplotlib.pyplot as plt
# Plot the observed and predicted values of the dependent variable
plt.scatter(y, model.fittedvalues)
plt.xlabel("Observed values")
plt.ylabel("Predicted values")
plt.title("Observed vs. predicted values")
plt.show()
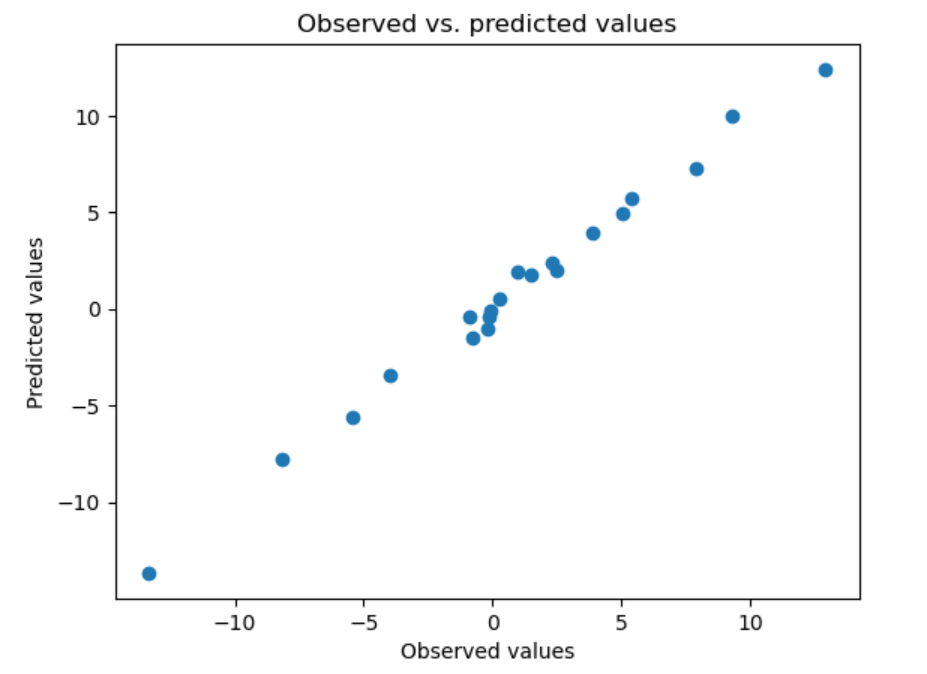
横軸に実データ、縦軸に予測値を取ったグラフです。
予測値と、実際の値の関係を可視化することで、今回作成した重回帰の精度をビジュアルで示すことができます。
まとめ
重回帰を用いた回帰モデル実装を解説しました。
もっともシンプルな重回帰を使いこなせるようになると、より高度な分析手法に取り組む足掛かりにもなります。身近なデータで、ぜひ一度トライしてみてください。
コメント